1 基础概念
1.1 傅里叶级数
1 周期函数
若函数f(x)满足:存在非零常数T,对任意x有f(x+T) = f(x),则称f(x)为周期函数,T为其周期;最小正周期称为基本周期(记为T0)。傅里叶级数中,最常用以2π为周期的函数(T=2π),其他周期的函数可通过变量替换转化为2π周期,因此核心研究2π周期函数。
2 三角函数系的正交性
傅里叶级数的本质是在三角函数系中对周期函数做正交分解,类似平面向量在x、y轴上的分解,三角函数系就是周期函数空间的一组正交基。
(1)标准正交三角函数系(2π周期)
{1,cosx,sinx,cos2x,sin2x,…,cosnx,sinnx,…}
其中n为正整数,1可以看作cos0x。(2)正交性的定义 对上述三角函数系中任意两个不同的函数φm(x)和φn(x),满足:
对同一个函数,积分结果非零:
(3)核心正交积分公式
正交性的意义:三角函数系中的各个基函数“互不干扰”,分解后的每个正余弦项的系数可独立计算,这是傅里叶级数能求解的关键。
3 傅里叶级数
法国数学家傅里叶认为,任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示(选择正弦函数与余弦函数作为基函数是因为它们是正交的),后世称傅里叶级数为一种特殊的三角级数,根据欧拉公式,三角函数又能化成指数形式,也称傅立叶级数为一种指数级数。在数学中,三角级数是任何具有下述形式的级数:
当An和Bn具有以下形式时,该级数称为傅立叶级数:
其中f(x)是可积函数。下面给出2π周期函数的傅里叶级数定义:
设f(x)是以2π为周期的函数,且在[-π, π]上可积,则其傅里叶级数为:
符号说明:
~:表示“展开为傅里叶级数”,而非严格相等(需满足收敛条件才相等);
a0/2:直流分量/零频项,是函数f(x)在一个周期内的平均值;
ancos nx:余弦项/偶次谐波,对应周期函数的偶函数分量;
bnsin nx:正弦项/奇次谐波,对应周期函数的奇函数分量;
a0, an, bn:傅里叶系数,是唯一确定的常数,有f(x)决定。
1.2 傅里叶变换
1 欧拉公式(Euler’s formula)
其中:e是自然常数,约等于2.71828,i是虚数单位满足i2=-1,θ是复指数的辐角∈R,对应复平面上的旋转角度。对于该公式当θ=π时,有eiπ + 1 = 0,这个公式在傅里叶变换中起到关键作用。
2 傅里叶变换(Fourier Transform, FT)
傅里叶变换是将时域的连续函数映射到频域连续函数的数学变换,是调和分析的核心工具,揭示了“任意连续周期/非周期函数均可分解为不同频率的正弦/余弦函数叠加”的本质。现给出连续傅里叶变换(Continuous Fourier Transform, CFT)相关定义,适用于定义域为全体实数R、满足狄利克雷条件(Dirichlet)的连续函数f(t),其中t为时域自变量(通常表示时间),变换后得到频域函数F(ω),ω为角频率(rad/s)。
(1)正变换(时域→频域)
积分区间(−∞,+∞)对应非周期函数的时域是无限的,需对全体实数域积分,变换本质是:用所有频率的复指数函数作为“基函数”,对f(t)做投影。
(2)逆变换(频域→时域)
傅里叶变换是可逆变换,从频域函数F(ω)还原时域f(t)的公式为:
关键系数1/2π:该系数是为了满足“正逆变换的归一性”,也有教材将系数拆分为1/sqrt(2π)分别放在正、逆变换中(数学上更对称),两种形式等价。
3 离散傅里叶变换(Discrete Fourier Transform,DFT)
DFT是一种线性变换,把一个有限长的离散序列,从“时间/系数域”变换到“频率/点值域”。其数学定义为给定长度为n的复数序列:x=(x0, x1, ..., xn-1),令:ω = e-2πi/n,定义其离散傅里叶变换(DFT)为序列:
xj是输入序列(时域信号),Xk是输出序列(频域信号),通过将时域信号与一系列不同频率的复指数函数进行内积,得到每个频率分量在原始信号中的“含量”。DFT是一个线性变换,本质是X = F*x,其中F是一个范德蒙德(Vandermonde)矩阵,即从线性代数角度看:DFT = Vandermonde变换。从矩阵运算可以看出,要得到每个频率分量,需要进行n次乘法和n-1次加法运算,完成整个变换需要n2次乘法和n(n-1)次加法运算,所以完整变换的复杂度是O(n2),当序列长度n较大时,计算量会变得极其庞大,限制了DFT在实际应用中的效率。
以多项式A(x)=a0+a1x+a2x2+...+an-1xn-1为例,则上述离散序列可以看作是多项式系数表示法(coefficient form)中的系数,即x = a = (a0, a1, ..., an-1),选择特殊的“点”——n次单位根:ω = e2πi/n,它满足:
以n=11为例,图中所有ωi都是11次单位根:
考虑n个互不相同的点:1, ω, ω2, ..., ωn-1,将其代入A(x)多项式,则有:
可见Xk = A(ω-k),即DFT的计算结果,恰好等价于在单位根上的多项式求值(对应多项式的点值表示法)。
逆离散傅里叶变换(IDFT)由以下公式给出:
傅里叶级数、傅里叶变换和DFT区别由下表给出:
4 快速傅里叶变换(Fast Fourier Transform,FFT)
1965年,J.W.库利和T.W.图基提出了著名的Cooley-Tukey算法,即快速傅里叶变换(FFT)。FFT算法的核心是利用旋转因子的周期性、对称性和可约性,将长序列的DFT分解为短序列的DFT,从而大幅减少计算量。首先给出单位根的三个引理:
一句话概括FFT:利用n次单位根的周期性与对称性,把一个规模为n的DFT,拆成两个规模为N/2的DFT。在经典FFT算法(Cooley-Tukey算法)中假设n=2m,把序列拆成“偶数项+奇数项”:
则可以将DFT拆开:
利用折半引理可将上式简化为:
其中:
以上将1个包含n次乘法的DFT分成两个n/2次乘法的DFT,另外由ωnn/2+k = -ωnk可以进一步得到迭代公式(1):
以上就是所谓的蝶形运算(butterfly),一次算出两个输出。可见一个长度为n的DFT被拆成两个长度是n/2的DFT和n/2次蝶形合并,所以时间复杂度为:
这里2T(n/2)表示:要解决一个规模为n的问题,需要“调用两次”规模为n/2的同类问题,每一次的代价是T(n/2);cn表示:当前这一层,为了把两个子FFT的结果“合并”所做的计算量。一个标准的radix-2蝶形:
需要:1次复数乘法ωb和2次复数加减法,都是常数级操作可记为O(1),对于长度为n的FFT每一层有n/2个蝶形,所以每层蝶形计算量是n/2xO(1)=O(n),可以记为cn,这里的c就是一个蝶形需要多少个“基础运算”的常数因子。所以随着层数递增有以下时间复杂度推导:
递归终止条件是当:n/2k=1,这时k=log2n,上述推导最终结果为:T(n)=n*T(1)+cnlog2n,忽略常数得最终复杂度公式T(n)=O(nlog2n)。
以上给出了快速傅里叶变换,快速傅里叶逆变换(IFFT,Inverse FFT)定义及分析过程与正变换类似,为了公式简洁正变换分析过程取ω = e-2πi/n,实际上在严格的数学定义中一般取ω = e2πi/n(正向单位根),此时正变换和逆变换定义如下:
正变换用于拆解信号,获取在正交基上的投影,逆变换用于合成信号,完成正交基投影的叠加。
1.3 NTT(Number Theoretic Transform)
NTT = 在有限域/模整数环中进行的FFT,即NTT是把FFT中的“复数单位根”换成了“模意义下的单位根”,结构完全一致,只是“数域”不同。FFT主要存在3方面问题:用的是复数、有浮点误差、在密码学/大整数/精确多项式运算中不可接受,而NTT正好可以解决这些问题。NTT工作空间是有限域,通常选Fp,p是素数,所有运算都基于mod p,在NTT中,需要找ω(模p下的n次原始单位根),它满足:
设模数p,n|(p-1),ω是n次原始单位根,NTT相关定义如下:
和FFT相关对比如下:
2 算法实现
理解了FFT的数学原理后,我们需要将其转化为可执行的代码。FFT算法有多种实现方式,包括递归实现、迭代实现和基于特定平台的优化实现。
2.1 递归实现FFT
递归实现是最直观的FFT实现方式,它直接对应Cooley-Tukey算法的分治思想。递归算法不断将问题分解为更小的子问题,直到达到基本情况(2点或1点DFT)。
  - import numpy as npimport matplotlib.pyplot as plt# 设置字体,确保中文显示plt.rcParams['font.sans-serif'] = ['SimHei']plt.rcParams['axes.unicode_minus'] = Falsedef fft_recursive(x): """ 递归实现快速傅里叶变换 注意:输入向量x的长度必须是2的幂次 """ n = len(x) if n == 1: return x # 分别计算偶数索引和奇数索引元素的FFT even_fft = fft_recursive(x[0::2]) # 偶数索引 odd_fft = fft_recursive(x[1::2]) # 奇数索引 # 计算旋转因子 w = [np.exp(-2j * np.pi * k / n) for k in range(n//2)] # 组合结果 result = np.zeros(n, dtype=complex) for k in range(n//2): term = w[k] * odd_fft[k] result[k] = even_fft[k] + term result[k + n//2] = even_fft[k] - term return result# 测试递归FFTdef test_fft_recursive(): # 生成测试信号:50Hz和120Hz正弦波的叠加 fs = 1000 # 采样频率1000Hz t = np.linspace(0, 1, 1024) # 1秒时间,1024个点 signal = np.sin(2 * np.pi * 50 * t) + 0.5 * np.sin(2 * np.pi * 120 * t) # 计算FFT fft_result = fft_recursive(signal) # 计算频率轴 freqs = np.fft.fftfreq(len(signal), 1/fs) print(len(freqs)) # 绘制结果 plt.figure(figsize=(12, 4)) plt.subplot(1, 2, 1) plt.plot(t, signal) plt.title('原始信号') plt.xlabel('时间 (s)') plt.ylabel('幅度') plt.subplot(1, 2, 2) plt.plot(freqs[:len(freqs)//2], np.abs(fft_result[:len(fft_result)//2])) plt.title('频谱图') plt.xlabel('频率 (Hz)') plt.ylabel('幅度') plt.xlim(0, 200) plt.tight_layout() plt.show()if __name__ == "__main__": test_fft_recursive()
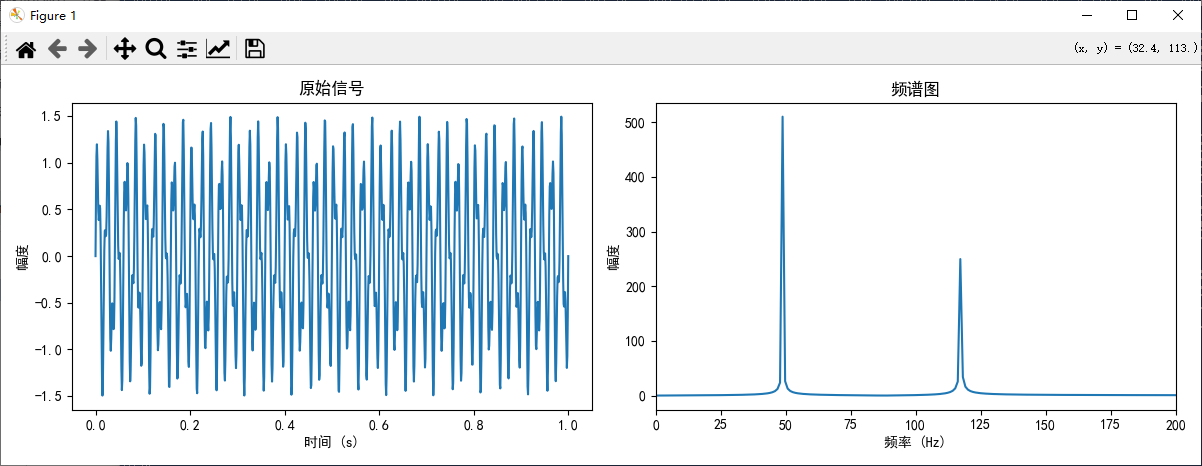
递归实现虽然直观,但存在一些缺点:
1. 递归调用会产生额外的函数调用开销
2. 需要不断创建新的子数组,内存使用不够高效
3. 对于大数组,可能导致递归深度过大
因此,在实际应用中,迭代实现通常更受青睐。
2.2 迭代实现FFT
迭代FFT算法通过循环而非递归实现计算,效率更高。迭代算法的核心是首先对输入数组进行位反序排列,然后通过多层循环实现蝶形运算。首先以n=8为例,看下X0的重排序,由于ω0=1则根据DFT公式可知:
观察以下二进制下标,可知重排序后的二进制下标正是正序下标二进制的逆序,把这种序列叫做逆二进制序:- 0 4 2 6 1 5 3 7000 100 010 110 001 101 011 111000 001 010 011 100 101 110 111 0 1 2 3 4 5 6 7
X0和X4完全对应迭代公式(1),实际上所有Xk计算过程可以由以下二叉树给出:
[code] 1 import numpy as np 2 import matplotlib.pyplot as plt 3 4 # 设置字体,确保中文显示 5 plt.rcParams['font.sans-serif'] = ['SimHei'] 6 plt.rcParams['axes.unicode_minus'] = False 7 8 def bit_reverse(n, num_bits): 9 """将n的二进制表示进行位反序""" 10 reversed_n = 0 11 for i in range(num_bits): 12 if n & (1 |