模拟退火算法

模拟退火算法

​    模拟退火算法最早的思想由Metropolis 等（ 1953 ）提出， 1983 年 Kirkpatrick 等将其应用于组合优化。
算法的目的：
克服优化过程陷入局部极小；
克服初值依赖性。
物理退火过程

在物理学中，退火是将金属加热到极高温度，然后让其极其缓慢地冷却的过程。

• 高温状态：原子运动剧烈，处于无序状态（高能量）。
  
• 等温过程  对于与环境换热而温度不变的封闭系统，系统状态的自发变化总是朝自由能减少的方向进行，当自由能达到最小时，系统达到平衡态；
  
• 缓慢冷却：原子逐渐找到最稳定的位置，形成整齐的晶体结构。
  
• 最终状态：系统的内能最低（全局最优）。
  

如果冷却得太快（淬火，Quenching），原子来不及调整位置就被“冻结”在杂乱的状态，系统处于亚稳态（局部最优，内能较高，材料脆）。
温度越低，物体的能量状态越低，到达足够的低点时，液体开始冷凝与结晶，在结晶状态时，系统的能量状态最低。缓慢降温（退火时，可达到最低能量状态；但如果快速降温（淬火，会导致不是最低能态的非晶形。
Boltzmann概率分布

在温度T，分子停留在状态r满足Boltzmann概率分布

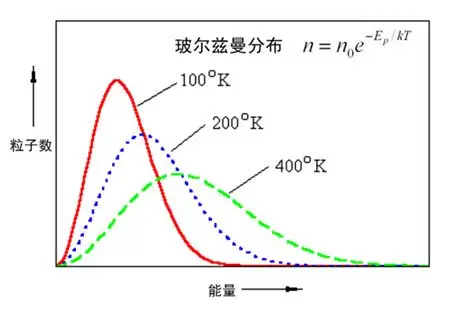
在同一个温度T，选定两个能量E1    auto solve(            const State& initial_state,            EnergyFunc energy_func,            Params params = Params{},            NeighborFunc neighbor = NeighborFunc{},            CoolingPolicy cooling = CoolingPolicy{},            ConstraintPolicy constraint = ConstraintPolicy{}    ) {        using AcceptancePolicy = MetropolisAcceptance;        detail::Solver                solver(params, energy_func, neighbor, cooling, AcceptancePolicy{}, constraint);        return solver.solve(initial_state);    }} // namespace sa#endif // SA_SA_HPP[/code]policies.hpp

1. #ifndef SA_SA_HPP
2. #define SA_SA_HPP
5. #include "params.hpp"
6. #include "policies.hpp"
7. #include "detail/solver.hpp"
9. namespace sa {
12.     /**
13.      * @brief 模拟退火通用求解函数
14.      * * @tparam State 状态类型 (自动推导)
15.      * @tparam EnergyFunc 能量函数类型 (自动推导)
16.      * @tparam NeighborFunc 邻域函数类型 (可选)
17.      * @tparam CoolingPolicy 降温策略 (可选)
18.      * @tparam ConstraintPolicy 约束策略 (可选)
19.      * * @param initial_state 初始状态值
20.      * @param energy_func 能量函数句柄
21.      * @param params 算法参数配置
22.      * @param neighbor 邻域生成器实例
23.      * @param cooling 降温器实例
24.      * @param constraint 约束器实例
25.      * @return std::pair<State, double> {最优状态, 最优能量值}
26.      */
27.     template<
28.             typename State,
29.             typename EnergyFunc,
30.             typename NeighborFunc = DefaultNeighbor<State>,
31.             typename CoolingPolicy = ExponentialCooling,
32.             typename ConstraintPolicy = std::nullptr_t
33.     >
34.     auto solve(
35.             const State& initial_state,
36.             EnergyFunc energy_func,
37.             Params params = Params{},
38.             NeighborFunc neighbor = NeighborFunc{},
39.             CoolingPolicy cooling = CoolingPolicy{},
40.             ConstraintPolicy constraint = ConstraintPolicy{}
41.     ) {
42.         using AcceptancePolicy = MetropolisAcceptance;
44.         detail::Solver<State, EnergyFunc, NeighborFunc, CoolingPolicy, AcceptancePolicy, ConstraintPolicy>
45.                 solver(params, energy_func, neighbor, cooling, AcceptancePolicy{}, constraint);
47.         return solver.solve(initial_state);
48.     }
50. } // namespace sa
52. #endif // SA_SA_HPP

复制代码

params.hpp

1. #ifndef SA_POLICIES_HPP
2. #define SA_POLICIES_HPP
4. #include "params.hpp"
5. #include "detail/traits.hpp"
7. #include <cmath>
8. #include <random>
9. #include
10. #include <stdexcept>
11. #include <vector>
13. namespace sa {
15.     // 默认降温策略
16.     struct ExponentialCooling {
17.         inline double operator()(double T, const Params& p) const noexcept {
18.             return T * p.alpha;
19.         }
20.     };
23.     // 默认接受策略 (Metropolis 准则)
24.     struct MetropolisAcceptance {
25.         template<typename RNG>
26.         bool operator()(double delta_E,
27.                         double T,
28.                         RNG& rng,
29.                         std::uniform_real_distribution<double>& dist) const
30.         {
31.             if (delta_E < 0.0) return true;
32.             return std::exp(-delta_E / T) > dist(rng);
33.         }
34.     };
37.     // 默认连续邻域生成策略
38.     template<typename State>
39.     struct DefaultNeighbor {
40.         double sigma = 1.0;
42.         State operator()(const State& current,
43.                          double T,
44.                          std::mt19937& rng) const
45.         {
46.             if constexpr (std::is_arithmetic_v<State>) {
47.                 std::normal_distribution<double> dist(0.0, sigma * T);
48.                 return static_cast<State>(current + dist(rng));
49.             }
50.             else if constexpr (detail::is_std_vector_v<State>) {
51.                 using ValueType = typename State::value_type;
52.                 static_assert(std::is_arithmetic_v<ValueType>,
53.                               "vector value type must be arithmetic");
55.                 std::normal_distribution<double> dist(0.0, sigma * T);
56.                 State candidate = current;
57.                 for (auto& v : candidate)
58.                     v = static_cast<ValueType>(v + dist(rng));
59.                 return candidate;
60.             }
61.             else {
62.                 static_assert(sizeof(State) == 0, "No default neighbor for this State type");
63.                 return current;
64.             }
65.         }
66.     };
69.     // 离散翻转邻域策略 (针对 vector<bool> 或 vector<int>)
70.     template<typename State>
71.     struct DiscreteFlipNeighbor {
72.         State operator()(const State& current,
73.                          double T,
74.                          std::mt19937& rng) const
75.         {
76.             static_assert(detail::is_std_vector_v<State>, "DiscreteFlipNeighbor requires std::vector");
77.             using ValueType = typename State::value_type;
79.             static_assert(
80.                     std::is_same_v<ValueType, int> || std::is_same_v<ValueType, bool>,
81.                     "DiscreteFlipNeighbor requires vector<int> or vector<bool>"
82.             );
84.             State candidate = current;
85.             std::uniform_int_distribution<std::size_t> dist(0, candidate.size() - 1);
86.             std::size_t idx = dist(rng);
88.             if constexpr (std::is_same_v<ValueType, bool>)
89.                 candidate[idx] = !candidate[idx];
90.             else
91.                 candidate[idx] = 1 - candidate[idx];
93.             return candidate;
94.         }
95.     };
98.     // 边界约束策略 (Box Constraint)
99.     template<typename State>
100.     class BoxConstraintPolicy {
101.     public:
102.         using ValueType = std::conditional_t<
103.                 std::is_arithmetic_v<State>,
104.                 State,
105.                 typename State::value_type>;
107.         BoxConstraintPolicy(ValueType lower, ValueType upper)
108.                 : lower_(lower), upper_(upper) {}
110.         void apply(State& state) const noexcept {
111.             if constexpr (std::is_arithmetic_v<State>) {
112.                 state = std::clamp(state, lower_, upper_);
113.             }
114.             else {
115.                 for (auto& v : state)
116.                     v = std::clamp(v, lower_, upper_);
117.             }
118.         }
120.     private:
121.         ValueType lower_;
122.         ValueType upper_;
123.     };
125. } // namespace sa
127. #endif // SA_POLICIES_HPP

复制代码

solver.hpp
[code]#ifndef SA_DETAIL_SOLVER_HPP#define SA_DETAIL_SOLVER_HPP#include "../params.hpp"#include #include #include namespace sa::detail {    template<            typename State,            typename EnergyFunc,            typename NeighborFunc,            typename CoolingPolicy,            typename AcceptancePolicy,            typename ConstraintPolicy    >    class Solver {    public:        Solver(Params params,               EnergyFunc energy,               NeighborFunc neighbor,               CoolingPolicy cooling,               AcceptancePolicy acceptance,               ConstraintPolicy constraint)                : params_(params),                  energy_(energy),                  neighbor_(neighbor),                  cooling_(cooling),                  acceptance_(acceptance),                  constraint_(constraint),                  dist_(0.0, 1.0)        {            validate_params();            if (params_.seed == 0) {                std::random_device rd;                rng_ = std::mt19937(rd());            } else {                rng_ = std::mt19937(params_.seed);            }        }        std::pair solve(const State& initial_state) {            State current = initial_state;            double current_energy = energy_(current);            State best = current;            double best_energy = current_energy;            double T = params_.initial_temp;            std::size_t total_iters = 0;            while (T > params_.final_temp && total_iters < params_.max_total_iters) {                for (std::size_t i = 0;                     i < params_.iter_per_temp && total_iters < params_.max_total_iters;                     ++i, ++total_iters)                {                    State candidate = neighbor_(current, T, rng_);                    // 编译期判断是否存在约束策略                    if constexpr (!std::is_same_v) {                        constraint_.apply(candidate);                    }                    double candidate_energy = energy_(candidate);                    double delta = candidate_energy - current_energy;                    if (acceptance_(delta, T, rng_, dist_)) {                        current = std::move(candidate);                        current_energy = candidate_energy;                        if (current_energy < best_energy) {                            best = current;                            best_energy = current_energy;                        }                    }                }                T = cooling_(T, params_);            }            return {std::move(best), best_energy};        }    private:        void validate_params() {            if (params_.initial_temp