彩笔运维勇闯机器学习--决策树

前言

决策树是一种常用的机器学习模型，用于分类和回归任务，它通过模拟“树”的结构来对数据进行决策。本节我们详细讨论的是决策树中的分类任务
开始探索

scikit-learn

假设以下运维场景

• CPU
  
  
  
  • 低：70%
    
  
  
• 内存
  
  
  
  • 低：85%
    
  
  
• 磁盘I/O
  
  
  
  • 低：70%
    
  
  
• 日志报错数（条）
  
  
  
  • 少：50
    
  
  

CPU内存磁盘I/O日志报错数系统是否稳定低低低少稳定中中低少稳定低中高少稳定低低低多不稳定低低高中不稳定高搞低少不稳定中高低中稳定高低低多不稳定中高高少不稳定中中中中不稳定高高低少稳定将其转换成代码：

1. import pandas as pd
2. from sklearn.tree import DecisionTreeClassifier
3. from sklearn.metrics import classification_report
6. level_map = {'低': 0, '中': 1, '高': 2, '少': 0, '中': 1, '高': 2, '多':2, '稳定': 1, '不稳定': 0}
7. data = [
8.     ['低', '低', '低', '少', '稳定'],
9.     ['中', '中', '低', '少', '稳定'],
10.     ['低', '中', '高', '少', '稳定'],
11.     ['低', '低', '低', '多', '不稳定'],
12.     ['低', '低', '高', '多', '不稳定'],
13.     ['高', '高', '低', '少', '不稳定'],
14.     ['中', '高', '低', '中', '稳定'],
15.     ['高', '低', '低', '多', '不稳定'],
16.     ['中', '高', '高', '少', '不稳定'],
17.     ['中', '中', '中', '中', '不稳定'],
18.     ['高', '高', '低', '少', '稳定'],
19. ]
21. data_mapped = [[level_map[v] for v in row] for row in data]
23. df = pd.DataFrame(data_mapped, columns=['CPU', '内存', '磁盘IO', '日志报错数', '系统是否稳定'])
25. X = df[['CPU', '内存', '磁盘IO', '日志报错数']]
26. y = df['系统是否稳定']
28. clf = DecisionTreeClassifier(criterion='entropy', random_state=0)
29. clf.fit(X, y)
30. y_pred = clf.predict(X)
32. print("分类报告：\n", classification_report(y, y_pred, target_names=['不稳定', '稳定']))

复制代码

脚本！启动

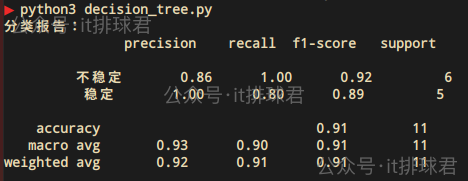
绘图更能直接观察决策树

1. from sklearn import tree
2. import matplotlib.pyplot as plt
4. plt.figure(figsize=(14, 8))
5. tree.plot_tree(clf,
6.                feature_names=['CPU', 'memory', 'storage I/O', 'error count'],
7.                class_names=['not stable', 'stable'],
8.                filled=True)
9. plt.show()

复制代码

分析绘图

• 每个矩形框代表一个决策节点（叶子节点），比如第一个框，error count1.5的熵，由于全是不稳定，所以熵是0
  

计算加权熵：\(Entropy_{weighted}=\frac{9}{11}⋅0.991+\frac{2}{11}⋅0 \approx 0.811\)
信息增益：0.994-0.811=0.183
</ul>选择error count以0.5为划分点

• error count0.5有5条，稳定与不稳定的比例为[1, 4]
  
• 首先计算原始熵：上面已经计算过了，0.994
  
  
  
  • 再计算error count0.5的熵：\(Entropy_2=-(\frac{1}{5}⋅log_2\frac{1}{5}+\frac{4}{5}⋅log_2\frac{4}{5}) \approx 0.722\)
    
  
  
• 计算加权熵：\(Entropy_{weighted}=\frac{6}{11}⋅0.918+\frac{5}{11}⋅0.722 \approx 0.829\)
  
• 信息增益：0.994-0.829=0.165
  

综上所述，error count为特征，以1.5为划分点，是合适的选择。并且将每个特征的每个划分点遍历一遍，得出error count